发表于 | 分类于

nlp讨论班刚开始没多久
得从基础唠起
遂做了个简短的注意力ppt
做个简单的介绍

这里写图片描述
这里写图片描述
这里写图片描述
这里写图片描述
这里写图片描述
这里写图片描述
这里写图片描述
这里写图片描述

发表于 | 分类于

这篇文章本身是用于seq2seq任务的
其中亮点提出了一个Multi-head attention具有相当的启发意义

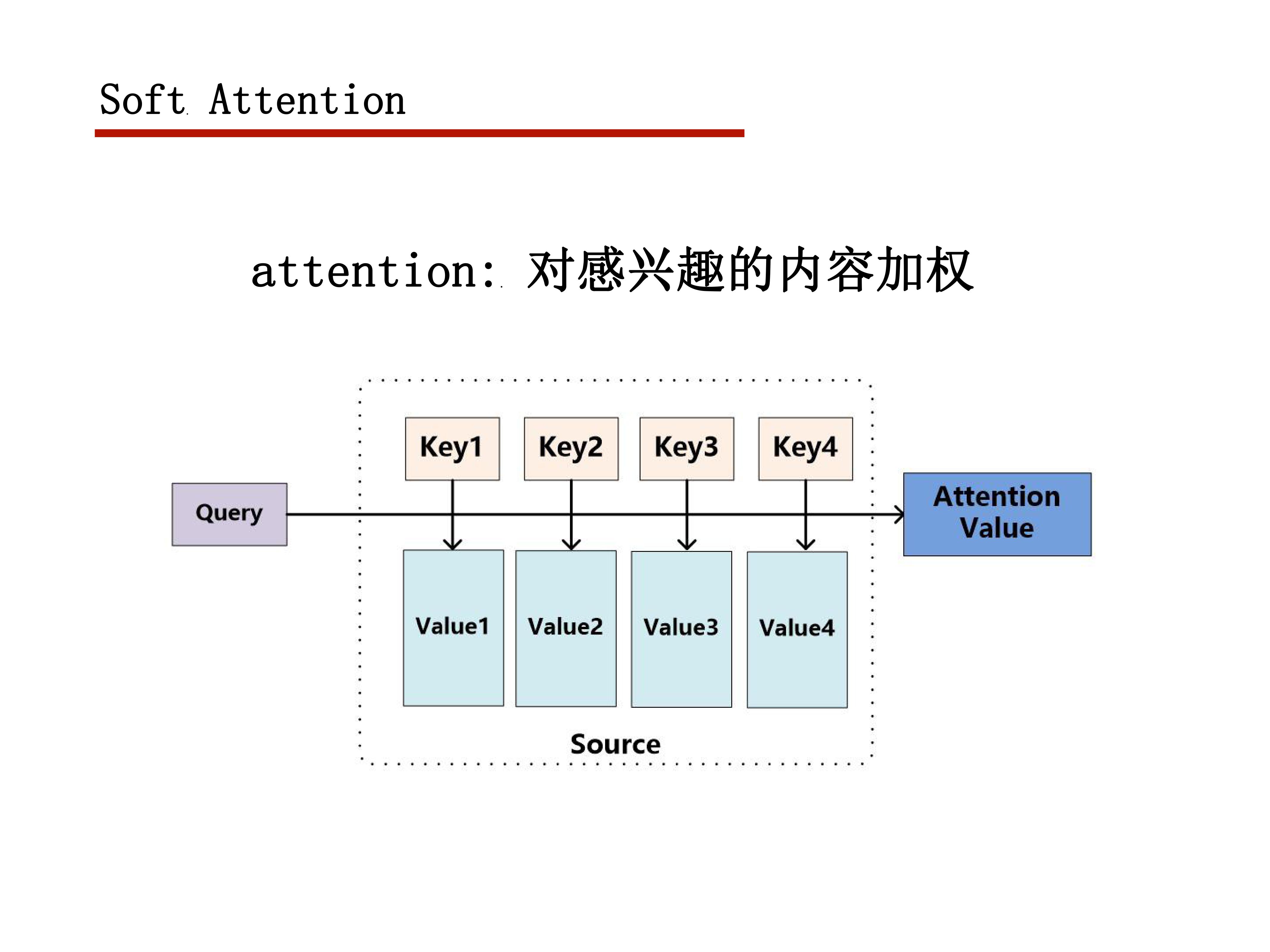
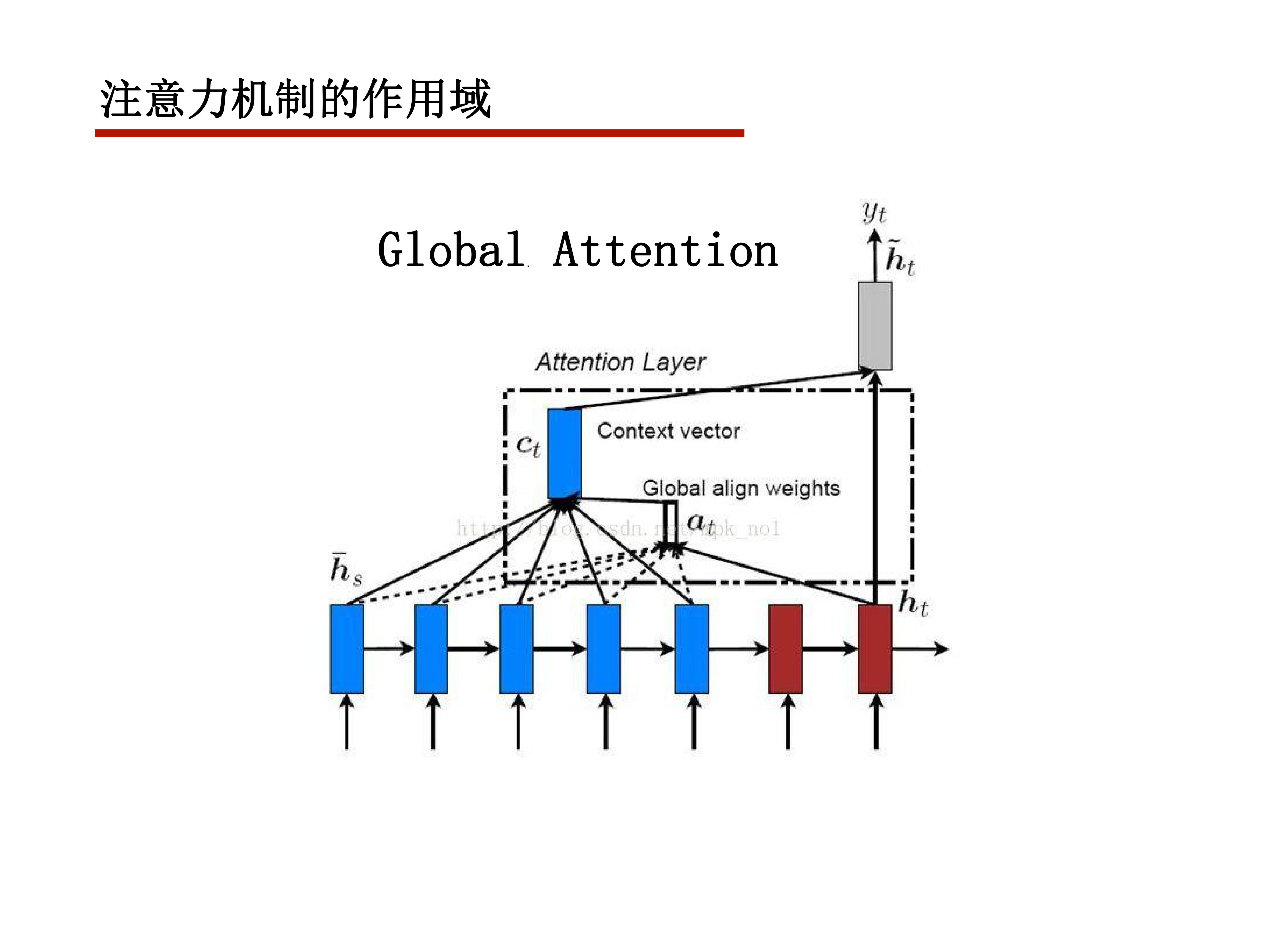
attention function

给定一个query
再给定一组(key,value)对,value可以理解为某个事物的具体信息,key为其关键信息

attention机制就是给出一组权重,使得模型对value的各个部分的关注度不同
这个关注度由query和key决定
很基本的想法就是和query越相关,权重越大

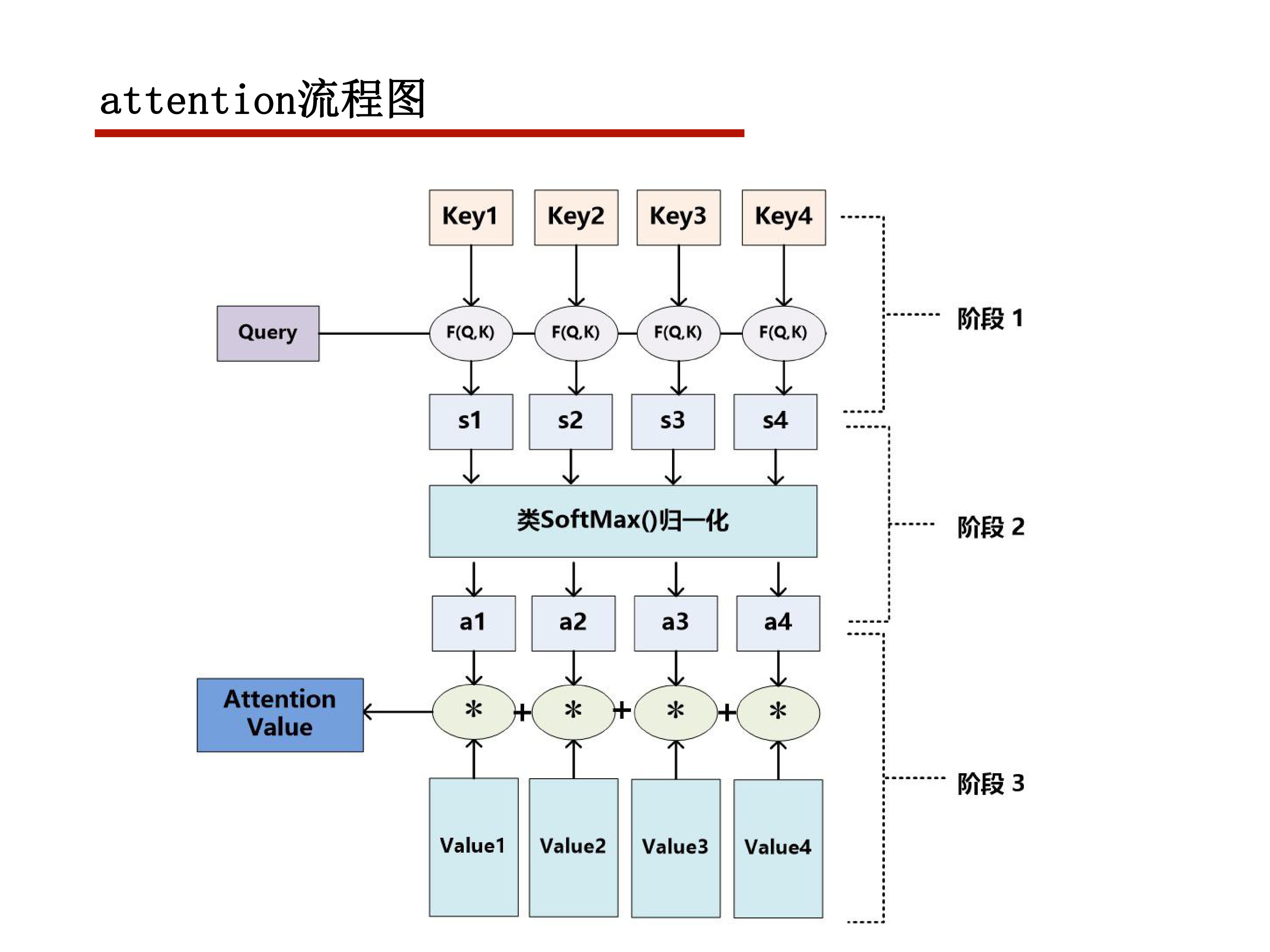
这里涉及到一个度量函数,常用的有余弦相似度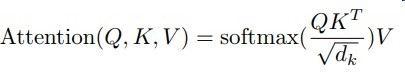
这里写图片描述
Q与K中的各个关键字做相似度计算,再进行权重归一化,对V进行加权求和获得最终内容
dk 是关键字的维度

获得权重后对value进行加权
大部分情况下key=value
个人认为当value维度过高时才需要关键信息的提取,这时才会有key和value的不同

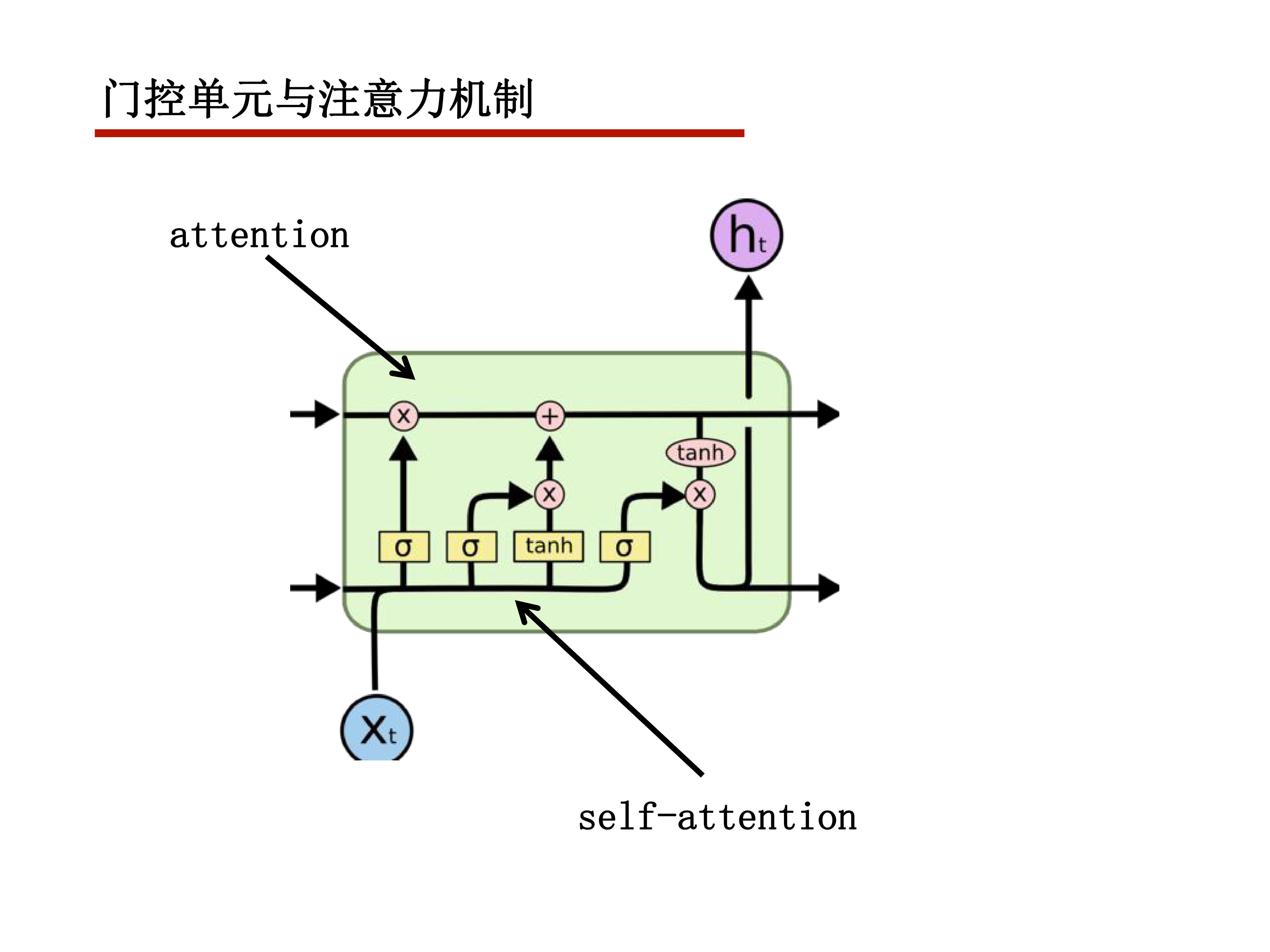
当key=value=query时,就是self-attention机制

Multi-Head Attention

这里写图片描述
首先用几个线性变换W将query,key,value映射到多个空间
再对他们通过注意力函数提取value的高质量信息

然后用h组线性变换W,进行拼接就得到了multi-head

Transformer

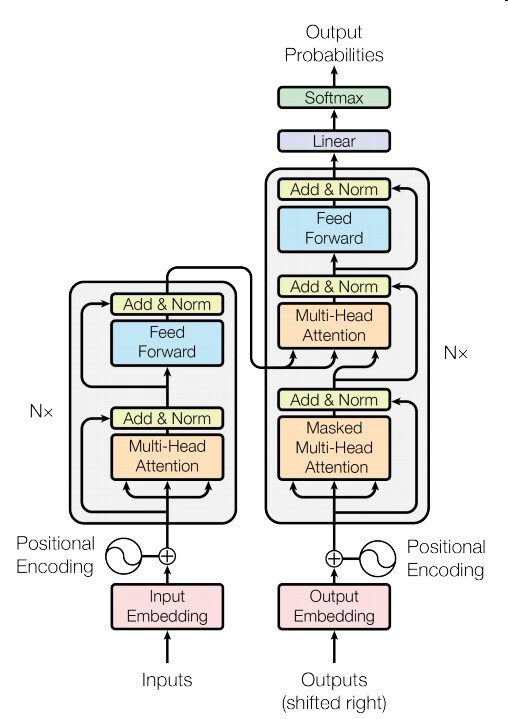
这里写图片描述
如上便是他的模型结构
左边是编码器,右边是解码器

Encoder

这个编码器由N=6个相同的组件堆叠而成
一个组件由两个子层组成

编码器的multi-head attention 是self-attention
Add & Norm是指残差连接和layer规范化

Feed Forward是指
FFN(x) = max(0,W1+b1)W2+b2
x是词向量

这就相当于两层kernel size = 1的卷积
或者时间步上共享权重的全连接层

Decoder

这个编码器由N=6个相同的组件堆叠而成
一个组件由两个子层组成

编码器的multi-head attention 是self-attention
Add & Norm是指残差连接和layer规范化

Feed Forward是指
FFN(x) = max(0,W1+b1)W2+b2
x是词向量

这就相当于两层kernel size = 1的卷积
或者时间步上共享权重的全连接层

output embedding

将上一时刻的预测作为当前输入
seq2seq的常用trick

position embedding

由于没有使用conv和rnn所以缺失位置信息
于是使用了一系列位置编码
其实看不大懂这个东西为啥work = =
见图

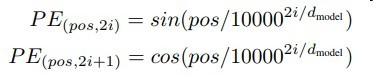
这里写图片描述

对于一个输入的句子矩阵(句长,词向量维度)
和他进行信息结合的是position以上述编码方式生成
i是第几个维度,pos是位置,时间轴
dmodel是词向量的维度

原本解释说这是因为PEpos+k可以表示为PEpos的线性函数

finally

这篇文章算是粗读
只理清了模型的推导
里面的参数设置和模型训练的具体细节没去纠

这篇文章对attention机制做了一个很好描述

发表于 | 分类于

模型结构

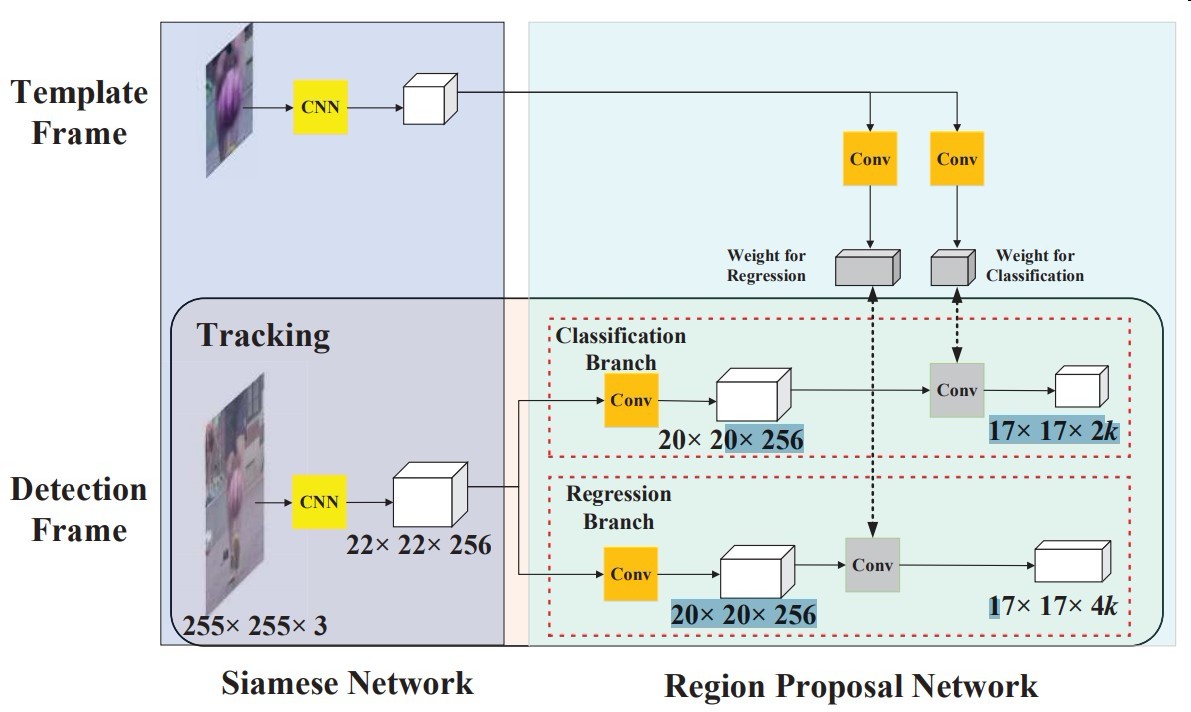
这里写图片描述

Siamese FC

使用AlexNet去掉conv2和conv4
所有卷积不使用padding

Region Proposal Network

其实看过faster rcnn 和 siamese fc还是一下子就能理明白的

  1. 模板帧用卷积抽成4×4×(2k×256)个代表k个anchor+前背景分类
  2. 模板帧用卷积抽成4×4×(4k×256)个代表k个anchor+坐标回归
    然后模板帧的特征图与检测帧的做相关运算进行匹配
    其中anchor比例为[0.33,0.5,1,2,3]

其中回归分支的需要,一些仿射变换用于做数据增强
然后proposed至少筛选16个正例,总共64个样本
正例IoU阈值为0.6,负例为0.3

然后loss照搬faster rcnn

one-shot detection

检测应用到追踪即为one-shot detection问题

推断

模板帧在第一帧推断后就不再更新了

  1. 第一帧的特征更鲁棒
  2. 速度快,nn慢就是因为要迭代bp
    所以这需要大量的数据进行预训练获得通用化的特征

proposal selection

  1. 不选取中心位置离当帧超过七个像素的anchor
  2. 给模型的分类置信度加penalty,其中k是超参,r和s分别代表了尺寸和面积,衰减尺度面积变化过大的anchor
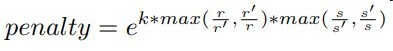
    这里写图片描述
  3. 选K个分类置信度最高的,进行NMS抑制
  4. 最终尺度选定后使用线性插值进行平滑改变

other details

使用VID和Youtube-BB数据进行离线训练
每次训练模板帧和检测帧之间的时间间隔不超过100帧

发表于 | 分类于

前言

最近忽然发现lightgbm中有个梯度优化的loss
以前一直好奇树模型如何对auc进行优化
于是查了一下,作此博文

AUC在梯度树与DNN中优化的不同之处

之前我在文章https://qrfaction.github.io/2018/04/02/end2endAUC/简述了DNN对AUC的优化方式
基本就是用一个度量函数将AUC公式中不可微的部分进行平滑

然而在梯度树中这带来了困难
见下图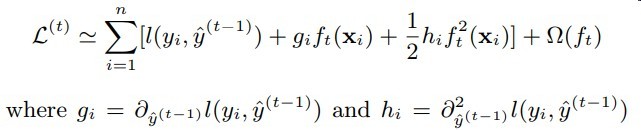
这里写图片描述
可知梯度树在计算梯度时主要获得的是针对每个样本的梯度信息
而原先在DNN中的AUC是无需将梯度细粒度到每个样本
只要有一个loss信息回传就OK了

可见原先的方式不再适用

Learning to rank 之 LambdaMART

MART其实就是GBDT(他名字很多诶)

这个方法其实是将rankLoss的梯度信息作为模型中的label y
即定义了模型的预测score的分数上升方向

首先定义一个rankLoss,其中si , sj是模型输出的score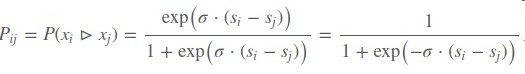
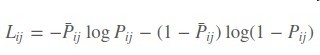
这里写图片描述
这里写图片描述

在对si求偏导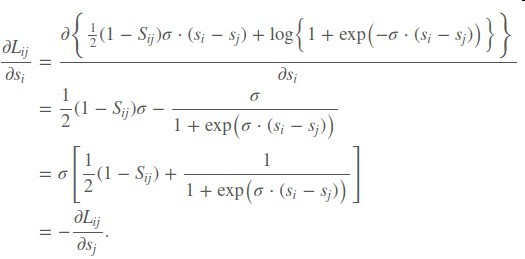
这里写图片描述
于是得到了一个si的上升/下降方向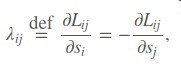
这里写图片描述
再令有序对(i,j)的排序label Sij = 1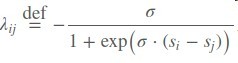
这里写图片描述
最后再将λi作为sample i的label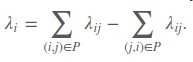
这里写图片描述

从而实现了树模型的Learning to rank

但这个我感觉应该对auc直接优化有很大帮助
因为毕竟auc本身也是一种基于排序的指标
但是否具有一致性就不清楚了
不过尝试了一下lightgbm中的lambda mart 训练速度超级慢…懒得试了

发表于 | 分类于

前言

最近有一些临时需求需要并行一些python代码
受限于multiprocessing的进程通信限制,不能很方便的通信大矩阵…

今天偶然发现一个Dask库
api与numpy,pandas一致,但可以并行计算
真的是雪中送炭hh

Dask

接口介绍

High Level

Arrays: 并行Numpy
Bags: 并行lists
Dataframes: 并行Pandas
Machine Learning : 并行Scikit-Learn
Others from external projects, like XArray

Low Level

Delayed: 用这个装饰器可以用于封装自定义函数来搭建计算图延迟计算
Futures: real-time parallel function evaluation

计算图搭建与延迟计算

方式一

import dask

lazy_results = []
for a in A:
  for b in B:
    if a < b:
      c = dask.delayed(f)(a, b) # 延迟任务计算,f是自定义函数
    else:
      c = dask.delayed(g)(a, b) # 延迟任务计算
    lazy_results.append(c)

results = dask.compute(*lazy_results) # 并行计算所有任务

方式二

@dask.delayed
def inc(x):
  return x + 1

@dask.delayed
def add(x, y):
  return x + y

a = inc(1) # 放入计算图
b = inc(2) # 放入计算图
c = add(a, b) # 放入计算图

c = c.compute() # 运行计算图并返回结果

Dask中的pandas一览

>>> import dask.dataframe as dd
>>> df = dd.read_csv(‘2014-*.csv’)
>>> df.head()
   x y
 0 1 a
 1 2 b
 2 3 c
 3 4 a
 4 5 b
 5 6 c

>>> df2 = df[df.y == ‘a’].x + 1

>>> df2.compute()
0 2
3 5
Name: x, dtype: int64

pandas中如下等各类函数皆被加速处理

dd.merge(df1, df2, on=’name’)
df.groupby(df.x).apply(myfunc)
df[df.x > 0]
df.x + df.y
等等

发表于 | 分类于

前言

最终结果是进决赛拿了二等奖
话说一等奖分数比我低很多诶,凭啥他一等= =
这个比赛其实从头水到尾,都没干啥事…
不过还是挑一些重点的有价值的东西讲讲
很多比赛总结其实一直好像是一个比较流水线的报告
从预处理到最后的集成
即便trick百出,仍似千篇一律

但我仍然喜欢有人能相对于trick提出更多的问题

下面只讲一下个人感觉有价值的东西
就不千篇一律的从数据预处理数据增强的一步步介绍了

比赛介绍

这个比赛是一个3D医学图像分割问题
目标是对大脑中的左右海马体进行分割

数据特点

132组样本
3D图像,4D张量,5D一个batchsize
十分吃显存
卷积核数稍微大一点就给你爆0.1T显存

训练不稳定
模型对海马体的差异十分敏感,不同的海马体dice loss差距对比有0.85 , 0.42

验证集阈值浮动
由于模型对海马体差异十分敏感
所以所以验证集分数经常会从几十跳成0

海马体强度不均
一些海马体体素强度在0至200的范围,部分在0至两千的范围

问题的解决方式

吃显存是真的没法子了
只能减通道数
毕竟换tesla P40是不可能的,这辈子都不可能换的
写插值压小图片又不想写,只能随随便便改改卷积核数才适合我

训练不稳定和验证集阈值浮动提供几个很棒的解决方案

  1. 改batchsize
    将batchsize设置为8问题就被缓解很多了,简单粗暴,但要牺牲一些通道数
  2. 将sigmoid激活改成tanh + score map MinMax归一化 + diceLoss
    这个方式超级显著,可以说完全解决了这个问题,小batchsize大概要几千轮的样子才能让loss和验证集稳定
    这个配合8 batchsize在仅仅600轮即可收敛到88的分数
    score map MinMax归一化是利用了图片中必定存在海马体的先验信息,即必定存在正例体素
  3. 一堆后处理trick(基于梯度,类间方差,类内方差,knn+先验等
    在这里我创了很多方法,这个方法有点慢,效果是有的,不如2+1
  4. ConvLSTM
    将3D图片的一个轴作为循环轴,利用循环单元拟合,这种结构契合了海马体的形态变化
    这个结构分数真的很稳,鲁棒性棒棒哒
  5. 在像素级的任务中尽量少用Pool,因为像素级的不对齐任务似乎还是有点影响的

summary

其他的事不想说了,毕竟水过来的,很不认真hh
一些数据增强,预处理都不想说了
我的几个模型结构也懒得聊,看多了只觉得模型结构要么是拍脑袋拿到的,要么是暴力搜素
毕竟缺乏理论性,马后炮式的分析结构是很抗拒的

发表于 | 分类于

本篇博客为高性能CUDA应用设计与开发第七章阅读笔记

CUDA上下文环境

cuda上下文环境

囊括了所必需的驱动状态信息,如虚拟地址空间,流,事件,已分配的内存块等

GPU设备与上下文

GPU设备驱动通过设备驱动程序为应用程序提供多个上下文环境
就可以使单个CUDA应用程序使用多个设备

同一时刻只能有一个上下文环境处于活动状态
所以需要操作多个设备时,需要用cudasetDevice()切换上下文环境

cuda在第一次调用一个改变驱动状态的函数时会自动默认创建一个上下文环境
如cudaMalloc()
默认在 GPU 0 上创建上下文

上下文与流

cuda程序通过将操作排队到流中,管理任务和并行
创建上下文时会隐式的创建一个流,从而命令可以在设备中排队等待执行
cudaMemcpy ,kernel函数等都会自动放入默认流中串行执行

除非指定不同的流,kernel函数流的指定如下
kernel<<<nBlocks, nThreadsPerBlocks, 0,stream>>>(para)
第三个可填参数是共享内存大小的分配

当kernel函数之间需要并发执行时要使用多个流

任务并发与同步

显式同步

cudaEventRecord()
我的理解是他是往当前流中异步发送了一个任务(记录时间)
由于同一个流中的顺序执行,使得他在之前的任务完成之后才能将传入的事件标记为完成

cudaStreamSynchronize() //同步流与cpu线程
cudaDeviceSynchronize() //在cpu线程中同步所有流
cudaStreamWaitEvent() //等待某个事件结束后再执行该流上的任务(这个任务在cudaStreamWaitEvent调用之后指定)
cudaStreamQuery() //查询一个流任务是否完成

隐式同步

部分主机操作在其完成前会强制所有流暂停执行
在使用下面这些主机操作时需注意,它们可能会停止所有的并发操作

  1. 页锁定主机内粗的分配
  2. 设备内存的分配
  3. 设备内存设置
  4. 设备到设备的内存拷贝
  5. L1缓存与共享内存之间的配置转换

p.s. 我印象中内存的拷贝有异步api的

同一GPU并发执行kernel注意事项

运行多个kernel会改变索引的局部性
增加L2缓存的未命中率,甚至消除缓存的有效性
还会引入其他问题
如bank冲突和内存分区冲突

内存映射

这部分书上主要讲了页锁定内存
感觉没另一本书讲的详细,之前博客写了不复述了

发表于 | 分类于

并发

python的并发已经被诟病许久了
GIL锁导致线程级并发争用一个CPU
计算密集型任务在多线程的模式下根本做不到真正意义上的并发
导致python的多线程只适用于非计算密集型任务类似I/O等

避开这个劣势一般有两种策略
其一是使用multiprocessing将线程级转到进程级
其二便是使用C语言

multiprocessing的进程通信方式

multiprocessing开启一个子进程,两者传参的通信方式是使用pickle将参数序列化

pickle是一种python自带的对象序列化方法,类似json
不同之处

  1. pickle是python专有,json是通用型序列化方法
  2. pickle编码方式是二进制,便于I/O以及传输,而json可读性较高I/O方面速度较慢
  3. json只能序列化python中的部分对象,而pickle可以序列化大多数

在python中使用进程并发时隐藏了这些细节
但实际中他是以pickle进行传输数据
这就带来了下面的问题

multiprocessing的进程通信限制

struct.error: ‘i’ format requires -2147483648 <= number <= 2147483647

这是我将一个比较大的矩阵作为参数进行传输时带来的问题

其实一个空间占用极大的对象理当不该作为参数传输
但是进程不像线程没有共享内存的空间诶,写细了很麻烦
再次diss一下Python的并发

这个是触发了多进程中pickle中序列化大小的限制
对象过大无法被序列化 = =

如果一些特殊条件导致不方便直接在硬盘上I/O
还有什么方法给一个进程传送存储量大的数据呢

multiprocessing的进程的共享对象

进程的原则本是尽量避免数据共享…
但有些情况下又不好避免
理当当断则断

multiprocessing中实现了很多用于进程间数据共享的对象
如Queue, Array, Value, NameSpace等等

这些对象共享数据的方式是用过创建一个服务进程
然后其他进程访问相关数据的某部分时
服务进程将这部分数据序列化传输给该进程

这就达到了分批传输的方式

我们这里介绍一个Manager的对象管理方式

创建数据server进程以及给worker进程分配任务

with Manager() as manager :
   dataset = manager.list()
   dataset.append(matrix)
   …
   pool.apply_async(worker,args=( dataset, other para))

worker进程中使用数据

def worker(dataset, other para):
   matrix1 = dataset[0]
   matrix2 = dataset[1]
    …

这与一般的list不同之处在于
manager的list对象的数据访问是从server进程上访问的
dataset.append(matrix) 通过这行代码将数据分批放入server进程中
再在worker进程中 matrix1 = dataset[0] 分批取出

即可避免了过大的数据无法序列化的问题

发表于 | 分类于

Network embedding 是表示学习中很重要的一块
著名的算法有node2vec,line,SDNE,svd等等
这篇论文提出的模型主要是对社交网络中的三角闭包结构和社交网络的时间动态变化建模

Definition

点集 V = { v1,v2,…,vM }
边集 E = { eij }

动态网络 G = { G1,G2,…,GT}
Gt = ( V , Et , Wt ) 表示每个时间段的网络图,Wt是权重
uti = ft(vi) 表示学习到的结点vi向量

Triadic closure process 三元闭包过程

以社交网络为例
( vi,vj,vk)在某时间段是个(open traid)开三角
即i,j互不认识,但k认识他俩
三元闭包过程就是以预测下一个时间段i,j会相识的概率
这个概率取决于k与他们的亲密程度
一般来讲越亲密越容易介绍他俩彼此相识
亲密程度建模如下,w为权重

其中下个时间段相识的概率为

极大似然估计

αijkt 为label ,下一时刻( vi,vj,vk)为(close traid)闭三角则为1,反之为0

再遍历所有open traid的样本组累乘概率进行极大似然估计
loss函数为

S+ 是下一段时刻会变成close traid的样本组集合
S- 相反

Social homophily


Et- 为Et中不存在的边
h(w,x) = wx
[ x ]+ = max(0,x)
该loss即使用了 tripet loss 期望近邻结点相似,非近邻结点稍远

Temporal smoothness

基于结点随时间的动态变化是平缓的猜想

final

最终三个loss加权求和即为最终loss

发表于 | 分类于

由于最近刚好由于要求写了一下PCA
其实还是很简单的
本篇介绍一个jacobi的方法

令X样本集,行向量为样本,列向量为特征

  1. 先对X的特征进行中心化, 即每一列特征减去其期望(均值)

  2. 奇异值分解

    X = Un,n Σn,m VTm,m
    选取奇异值最大的 k 个主成分,即
    X ≈ Un,k Σk,k VTk,m
    <=>
    X Vm,k ≈ Un,k Σk,k

    其中Un,k Σk,k 即为X的低维空间投影
    Vm,k为降维矩阵
    至此PCA过程就结束了

  3. 特征值分解与奇异值分解

    XTX = P λ PT = V ΣTΣ VT
    其中P是正交阵, λ 为特征值对角正阵, 特征值从大到小排序
    所以只需令P = V , ΣTΣ = λ 即可
    再用U = ΣT V X 即可求出 U

  4. 计算特征向量

    这里写图片描述
    基本想法是通过不断使用givens变换 (初等旋转变换) 将X的非对角元素变为0
    P = ∏i Pi (Pi 是givens变换)
    PT XTX P = λ
    其中Pi中未知量的选取见下图
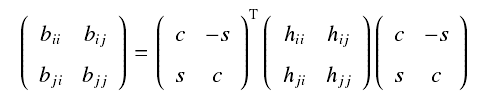
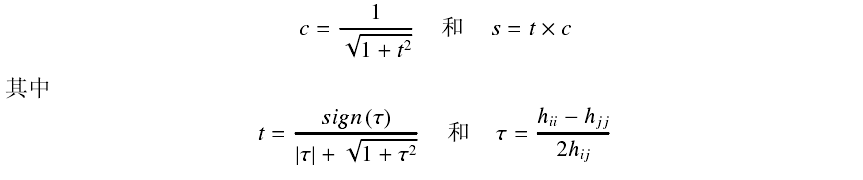
    这里写图片描述
    这里写图片描述

    接着直至收敛
    接着将λ中的特征值从大到小排序,P中的特征向量依据λ的顺序进行排序
    从而得到了V

    end 很简单hh 从头至尾就是一些矩阵乘法运算
    givens和X的乘法只涉及到两行两列的元素故为O(n)的复杂度