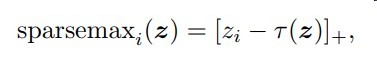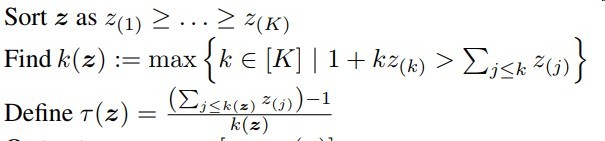这篇文章主要是稀疏性的需求而提出了一个带有稀疏特性的归一化函数sparsemax
常见的有 sigmoid/tanh -> hard_sigmoid/hard_tanh
sparsemax在二维情况即为hard_sigmoid
我认为稀疏特性是attention以后十分重要的发展方向
目前大部分的soft attention都是基于softmax
这就带来了一个缺点,每个元素都会对结果产生影响
而hard attention又带了难以优化的问题
自然而然sparse attention是一个很好的发展方向
虽然本篇文章我应用效果并不怎样…
但是仍然感觉很有启发意义
本篇文章稀疏化的方式是通过一个阈值
再利用max函数屏蔽掉一部分权重
其中[x]+指代max(x,0)
该阈值的好处
- 介于min(z)与max(z)之间,保证能屏蔽一部分与留下一部分
- k的选择保证了主要成分的保留
此函数需自定义梯度回传公式
梯度回传公式如下
其中S(z)为[z-r(z)]+中非0的部分
这个梯度公式意思很简单
即用到的部分回传梯度,没用到的部分梯度为0
sparsemax应用场景
- attention归一化权重
- 多分类