PCA实现

由于最近刚好由于要求写了一下PCA
其实还是很简单的
本篇介绍一个jacobi的方法

令X样本集,行向量为样本,列向量为特征

1. 先对X的特征进行中心化, 即每一列特征减去其期望(均值)

2. 奇异值分解

   X = U_n,n Σ_n,m V^T_m,m
   选取奇异值最大的 k 个主成分,即
   X ≈ U_n,k Σ_k,k V^T_k,m
   <=>
   X V_m,k ≈ U_n,k Σ_k,k

   其中U_n,k Σ_k,k 即为X的低维空间投影
   V_m,k为降维矩阵
   至此PCA过程就结束了

3. 特征值分解与奇异值分解

   X^TX = P λ P^T = V Σ^TΣ V^T
   其中P是正交阵, λ 为特征值对角正阵, 特征值从大到小排序
   所以只需令P = V , Σ^TΣ = λ 即可
   再用U = Σ^T V X 即可求出 U

4. 计算特征向量

   
   基本想法是通过不断使用givens变换 (初等旋转变换) 将X的非对角元素变为0
   P = ∏_i P_i (P_i 是givens变换)
   P^T X^TX P = λ
   其中P_i中未知量的选取见下图
   
   

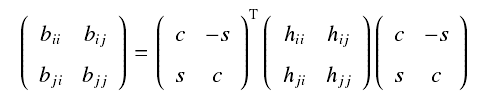
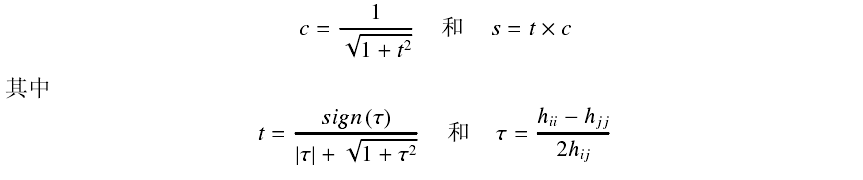
   接着直至收敛
   接着将λ中的特征值从大到小排序,P中的特征向量依据λ的顺序进行排序
   从而得到了V

   end 很简单hh 从头至尾就是一些矩阵乘法运算
   givens和X的乘法只涉及到两行两列的元素故为O(n)的复杂度