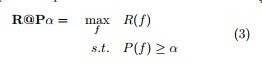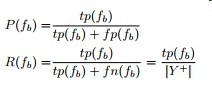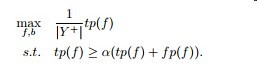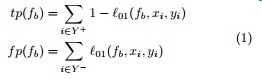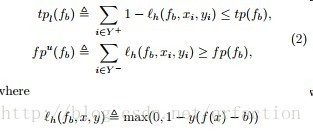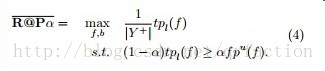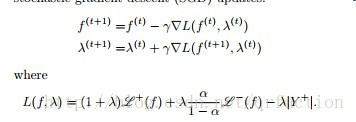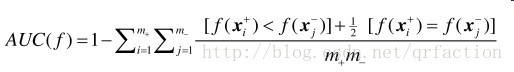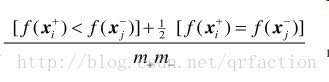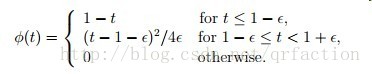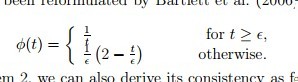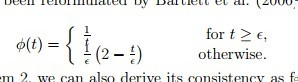AUC与F-score的直接梯度优化
此博文为 本人 CSDN博客迁移过来
原文链接 https://mp.csdn.net/mdeditor/79218697
AUC与F-score作为分类问题竞赛中热门的评估指标
对于他们的优化往往都是通过间接方法
例如样本不平衡中的代价敏感学习
对于auc与F-score的介绍不在展开
附上网上找的一个链接https://www.jianshu.com/p/498ea0d8017d
一个论文中提到的方法
论文链接 http://proceedings.mlr.press/v54/eban17a/eban17a.pdf
这里f-score的优化方式是约束精准率的下限来最大化召回率实现的
论文里废话比较多 挑些重点放 详细看论文吧
以F1-score为例
优化目标与精准率召回率公式:
`等价转换
将零一损失替换会hinge损失便于优化 这里的Lh 是hinge损失
优化目标变为
再等价转换
拉格朗日函数
梯度优化法其基本想法其实是用Hinge替代了零一损失
所以直接优化f-score的关键点在于找到一个可凸优化的loss来替代召回率精准率
而固定精准率最大化召回率等比较次要
找到了这个loss后直接使用框架带有自动求导机制梯度优化即可
AUC的优化
auc是一个基于rank的评价指标
下面先给出auc的计算公式
基于上面论文的思路 我们只需要将里面不可微的部分用一个函数去平滑他即可
观察下图
正例 < 负例 loss =1
正例 = 负例 loss=0.5
正例 > 负例 loss=0
可以用对数loss , 指数loss , 均方误差等loss替代
但是不是所有loss替代后和原AUC的优化有一致性https://arxiv.org/pdf/1208.0645.pdf
这篇论文指出 有如下与auc有一致性的loss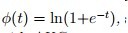
综上 我们知道了NN可以 end-to-end的优化auc与f-score了
可是基于GBDT及其改版的梯度树似乎没有什么好的办法直接优化?
梯度树将样本的一阶至二阶梯度信息替代了信息熵和基尼指数来作为评分函数
梯度信息将决定样本归于哪个叶节点
而这里的优化方式是计算了样本总体的一个loss
无法区分到各样本上
貌似树模型的auc与F-score优化还是只能靠剪枝?